Una multiplicación es una suma de varios sumandos iguales.
15 + 15 + 15
+ 15 = 60 -------------- 14 x 4 = 60
* Los términos de la multiplicación se llaman factores y el resultado, producto.
Los signos de la multiplicación son
(x) y (.)
PROPIEDADES DE LA MULTIPLICACIÓN:
1- Conmutativa: el orden de los
factores no altera el resultado final.
8 x 6 = 6 x 8
2- Asociativa: podemos agrupar los factores
de diversas maneras sin que varíe el resultado.
2 x ( 6 x 4 ) = ( 2 x 6 ) x 4
3- Distributiva : El producto de un
número por una suma es igual que la suma de los productos del número por los
sumandos.
4 x ( 8 + 3 ) = ( 4 x 8 )+ ( 4 x 3 )
*Elemento neutro: Es el número uno ( 1 ) ,
porque cualquier número multiplicado por 1 , da el mismo resultado.
MULTIPLICACIONES
ESPECIALES:
*Por la unidad
seguida de ceros:
Se añaden a la derecha del número tantos ceros como
números hay.
*Multiplicación de
números que acaban en ceros:
Se multiplican los números sin los ceros
finales y después se añaden al resultado los ceros que tenían entre los dos.
3200 x 40 = 128000
*Ceros intermedios en el multiplicador:
* Primero
hemos multiplicado por cinco y posteriormente, en vez de multiplicar por el cero, lo que hacemos es multiplicar directamente por
el cuatro pero desplazando los números de la segunda fila de la multiplicación
dos lugares a la izquierda en vez de uno.
*Si los ceros
intermedios fueran 2 en vez de uno desplazaríamos la segunda fila de la
multiplicación 3 lugares a la izquierda.
Cómo resolver problemas con multiplicación:
¿Se te da bien resolver
problemas?
Resolver problemas es
una parte muy importante de
las matemáticas, porque con ellos entiendes y practicas lo
que has aprendido a hacer.
Hoy vamos a ver los problemas de multiplicación: ¿cómo los reconocemos? y
¿qué hay que hacer para resolverlos?
1. Problemas de multiplicación:
Repetición
Este es el primer tipo de problemas de multiplicación que se aprende a hacer.
Ana
tiene 5 cajas de huevos. Cada caja tiene 12 huevos.
¿Cuántos huevos tiene en total?
Encontraremos:
Para resolver este problema, debemos pensar:
-Si en cada caja hay 12
huevos y Ana tiene 5 cajas, para saber cuántos huevos hay en total, sumaremos
12 + 12 + 12 + 12 + 12 o, lo que es lo mismo, multiplicaremos 5 x 12:
-En
total, Ana tiene 60 huevos
2. Problemas de multiplicación:
Escalar de comparación
En este tipo de problemas de multiplicación se compara una cantidad con otra que
es más grande o más pequeña:
Para
comprar el regalo de su padre, Juan ha puesto 10.000 pesos y Patricia ha puesto 3
veces más dinero que él.
¿Cuánto dinero ha puesto
Patricia?
Encontraremos:
– Un número que expresa una cantidad: Juan ha puesto 10.000 pesos.
Para resolver el problema, debemos pensar:
Si Patricia ha puesto 3
veces más dinero que Juan, quiere decir que habrá puesto el triple de dinero.
Por eso, multiplicaremos 10.000 x 3:
Patricia ha puesto 30.000 pesos.
3. Problemas de multiplicación:
Escalar de fórmula
En este tipo de problemas de multiplicación nos aparecerán fórmulas, como por
ejemplo una velocidad:
Sergio
es conductor de autobús. Me ha dicho que, si no hiciese ninguna parada y
mantuviese siempre la velocidad de 80 kilómetros por hora, tardaría en hacer su
recorrido exactamente 2 horas. ¿Cuántos kilómetros mide su recorrido?
Encontraremos:
– Una velocidad: Si mantuviese la velocidad
de 80 kilómetros por hora
Para resolver el problema, debemos pensar: si mantiene
una velocidad de 80 kilómetros por hora, quiere decir que cada hora que conduce
recorre 80 kilómetros. También sabemos que conduce a esta velocidad durante 2
horas. Por lo tanto, para saber el número de kilómetros que recorre en total,
tendremos que multiplicar 80 x 2:
Su recorrido mide 160 kilómetros.
-En este tipo de problemas de
multiplicación encontraremos dos o más conjuntos de cosas o personas.
-Estos
conjuntos se deben combinar entre sí formado todas las parejas posibles:
Hoy
hemos ido a comer a un restaurante italiano especializado en pasta. Me ha
costado mucho decidir qué plato pedir, ya que en la carta había 9 tipos de
pasta y 11 tipos de salsa, y se podía pedir cualquier pasta con cualquier
salsa.
¿Entre cuántos platos distintos de pasta con salsa se podía elegir?
Encontraremos:
– El número de elementos que tiene el primer conjunto: 9 tipos de pasta
Para resolver el problema, debemos pensar:
-Cada tipo de pasta podríamos combinarla con los 11 tipos de salsa disponibles. Por lo tanto, solo con el primer tipo de pasta podemos obtener 11 platos distintos.
-Combinando el segundo tipo de pasta con cada una de las 11 salsas, también
obtendríamos otros 11 platos distintos. Es decir, por cada uno de los 9 tipos
de pasta, obtendremos 11 platos distintos al combinarlos con las salsas.
-Por
ello, para averiguar el número de platos posibles, multiplicaremos 9 x 11: Se podía elegir entre 99 platos distintos de
pasta
Problemas:
1.- En cada aula de un
colegio hay entre 25 y 30 sillas. Si en ese colegio hay 14 aulas. ¿Cuántas
sillas habrá como mínimo? ¿Y como máximo?
2.- Cuatro decenas de huevos
y seis huevos más. ¿Cuántos huevos son?
3.- Cuatro kilos de patatas
y 5 sacos de 6 kilos cada uno, ¿cuántos kilos de patatas son?
4.- Laura es piloto
comercial. Cada semana realiza cinco viajes de ida y vuelta entre Alicante y
Vitoria. La distancia entre ambas ciudades es de 730 Km. Laura estima que en
seis semanas recorre más de 40.000 Km, que es como dar la vuelta al mundo.
¿Tiene razón Laura?
5.- Un grifo estropeado pierde un litro de
agua cada media hora. ¿Cuánto perderá cada hora? ¿Cuánto perderá al cabo de un
día? Si no se repara. ¿Cuántos litros se perderán en un mes?
6.- Una camisa tiene siete
botones en la parte delantera, dos en el cuello, uno en cada puño y un botón de
repuesto. Si una fábrica hace cada día 20 camisas de manga larga y otras 20 de
manga corta. ¿Cuántos botones gastan en un día? ¿Tendrán suficiente con 2.000
botones para los cinco días de una semana?
7.- Una charca contiene
3.000 litros de agua, y en ella beben vacas y ovejas. Cada día, una oveja bebe
2 litros de agua y una vaca bebe 8 litros. Si al cabo de un día pasan por la
charca 253 ovejas y 117 vacas, ¿habrá agua para todas?
Dividir es
repartir un número en grupos iguales (del tamaño que indique el divisor).
Por ejemplo:
45 : 5 es repartir 45 en grupos de 5.
Los términos
de la división son:
· -Dividendo: es el número que vamos a dividir.
División por una cifra:
Por ejemplo:
-Queremos repartir 243 caramelos entre 5
amigos.
-El dividendo será 243 porque es la cantidad que queremos dividir.
-El
divisor es 5 porque es el número por el que queremos dividir (repartir) los 243
caramelos.
-El cociente será el número de caramelos que recibe cada niño y el
resto son los caramelos que sobran.
Vamos a ver los pasos para calcular el cociente y el
resto:
1. Cogemos la primera cifra del
dividendo. Si esta cifra es más pequeña que el divisor, entonces tendremos que
coger otra cifra más del dividendo.
En nuestro ejemplo la primera cifra del dividendo es
2, pero como es más pequeña que el divisor, que es 5, tenemos que coger otra
cifra más: 24
2. Buscar un número que al
multiplicarlo por el divisor nos dé como resultado el dividendo. Si no lo hay,
buscamos el resultado menor más próximo. El resultado de la multiplicación se
resta al dividendo.
-Nosotros tenemos que dividir 24 entre 5.
Buscamos un
número que multiplicado por 5 me dé 24. Como no es exacto buscamos el menor más
próximo: 4 x 5 = 20.
-En este caso, 20 es el número más cercano a 24 siendo
menor. Por lo tanto escribimos el 4 en el cociente y el 20 se lo restamos a 24,
y 20 – 24 = 4
3. Bajar la siguiente cifra del dividendo y realizar de nuevo el paso
2.
-Bajamos la siguiente cifra que es el 3. Con el 4 que
ya teníamos y con el 3 que acabamos de bajar obtenemos el 43.
Por lo tanto, cada niño recibe 48 caramelos y sobran 3
caramelos sin repartir.
División por dos o tres cifras:
Para
hacer divisiones de dos o tres cifras hay que seguir los siguientes pasos:
1- Coger tantas cifras del dividendo como cifras tenga el
divisor. Si las cifras del dividendo son más pequeñas que el divisor, hay que
coger otra cifra más en el dividendo.
Por
ejemplo:
Si queremos dividir 5738 / 73, lo primero que tenemos que hacer es
coger dos cifras del dividendo, 57, pero como 57 es menor que 73, hay que coger
otra cifra más del dividendo, es decir, 573.
2- Dividir el primer número del dividendo (o los dos
primeros si hemos tenido que coger otra cifra) entre el primer número del
divisor y comprobar si cabe. Si no cabe, comprobar con el número anterior.
-Si
seguimos con el ejemplo anterior, tendríamos que dividir 57 entre 7. Como 8 x 7
= 56, probaremos con 8.
-Multiplicamos 73 x 8 = 584 y como 584 es mayor que 573,
el 8 no cabe, por lo que tendríamos que probar con el número anterior.
-Seguimos
con nuestro ejemplo de división por dos cifras. El siguiente número que
tendríamos que bajar es el 8, por lo que ahora tendríamos que dividir 628 entre
73.
Cómo resolver problemas de divisiones:
Vamos a plantear varios problemas diferentes que
requieran de una división para su resolución.
Problema 1.
*Este es el tipo de problema más fácil que nos podemos
encontrar sobre divisiones. El problema nos dice que hay 18 cajas y se quieren repartir a partes iguales entre 9 clases.
Cuando hablemos de repartir
a partes iguales estamos hablando de DIVIDIR.
R//. Cada clase recibirá 2 cajas de gomas de borrar.
Problema
2.
En el
depósito de agua que hay al lado de los grandes jardines de mi pueblo en lo más
alto de una colina, que está ahí para que haya suficiente agua para los riegos,
solo quedan 56 litros de agua. Si se reparte
toda en recipientes de 8 litros cada uno,
¿cuántos
recipientes se llenarán?
Este problema es parecido al anterior. De nuevo hay
que repartir los 56 litros de agua en
recipientes de 8 litros cada uno. Por lo tanto, lo que tenemos que hacer es DIVIDIR.
56: 8 = 7
R//. Se llenarán 7 recipientes.
Problema
3.
Como
todos los domingos por la mañana, Ricardo y Catalina han salido a andar por el
campo. Como están acostumbrados a hacer deporte, van rápido y sin hacer paradas
en el camino.
Sabiendo
que la caminata dura 3 horas, que en total caminan 15 kilómetros y que se han
cruzado con 7 personas, calcula a qué velocidad caminan.
Hay que empezar aclarando en este problema que la
velocidad se mide en km/h (se lee kilómetros por hora), y se refiere a los
kilómetros que se recorren en una hora.
Para hallarlo tendremos que DIVIDIR.
R//. Ha ido a una velocidad de 5 km/h.
Problema
4.
Raimundo
y yo estamos ahorrando para comprar un juego entre los dos y regalárselo a
Carmen por su cumpleaños, que va a ser dentro de 5 días. Él ha conseguido 90.000 pesos y yo ya tengo 270.000
¿Cuántas
veces he ahorrado yo más dinero que Raimundo?
El lenguaje del problema puede llevar a
interpretaciones erróneas, ya que veces más o veces menos puede interpretarse
como una suma o resta pero siempre van asociados a problemas de
multiplicaciones o divisiones.
Yo he ahorrado 3 veces más dinero que Raimundo.
Potencia
de un número es multiplicar dicho número por sí mismo tantas veces como indique
el exponente.
*La potencia se lee "base elevado al exponente".
Los 3 ejemplos anteriores se leen:
2 elevado a 5
*Potencia en base 10
Como se puede
apreciar en los ejemplos anteriores, en la potencia en base 10 el resultado
siempre es igual a 1 seguido de tantos ceros como indique el exponente.
En el primer
ejemplo un 1 seguido de 5 ceros
La radicación es en realidad otra forma de
expresar una potenciación.
La raíz de cierto orden de un número es
equivalente a elevar dicho número a la potencia inversa.
Por esto, las propiedades de
la potenciación se cumplen también con la radicación. Para que estas
propiedades se cumplan, se exige que el radicando de las raíces sea positivo.
• Es distributiva con respecto a la multiplicación y a la
división.
Veamos un ejemplo:
-En la división
-En la multiplicación
• No es distributiva con respecto
a la suma y a la resta.
Ejemplos:
En la suma
• Si el índice es par entonces el
radicado tiene que ser positivo y la raíz entonces dos
resultados, uno positivo y otro negativo, para este nivel utilizamos el
resultado positivo.
Ejemplos
Si el índice es impar entonces la raíz va
a tener el mismo signo que el radicando:
Si tengo una raíz de raíz se multiplican
los índices:
*Elemento neutro: Es el número uno ( 1 ) ,
porque cualquier número multiplicado por 1 , da el mismo resultado.
MULTIPLICACIONES
ESPECIALES:
*Por la unidad
seguida de ceros:
Se añaden a la derecha del número tantos ceros como
números hay.
8 x 100 = 800 28 x 1.000 = 28.000
*Multiplicación de
números que acaban en ceros:
Se multiplican los números sin los ceros
finales y después se añaden al resultado los ceros que tenían entre los dos.
3200 x 40 = 128000
*Ceros intermedios en el multiplicador:
* Primero
hemos multiplicado por cinco y posteriormente, en vez de multiplicar por el cero, lo que hacemos es multiplicar directamente por
el cuatro pero desplazando los números de la segunda fila de la multiplicación
dos lugares a la izquierda en vez de uno.
*Si los ceros
intermedios fueran 2 en vez de uno desplazaríamos la segunda fila de la
multiplicación 3 lugares a la izquierda.
Cómo resolver problemas con multiplicación:
¿Se te da bien resolver
problemas?
Resolver problemas es
una parte muy importante de
las matemáticas, porque con ellos entiendes y practicas lo
que has aprendido a hacer.
Hoy vamos a ver los problemas de multiplicación: ¿cómo los reconocemos? y
¿qué hay que hacer para resolverlos?
1. Problemas de multiplicación:
Repetición
Este es el primer tipo de problemas de multiplicación que se aprende a hacer.
Por ejemplo:
Ana
tiene 5 cajas de huevos. Cada caja tiene 12 huevos.
¿Cuántos huevos tiene en total?
Encontraremos:
– Un número de conjuntos: Ana tiene 5 cajas de huevos
– El número de cosas que hay en cada conjunto: Cada caja tiene 12 huevos
– La pregunta sobre el número de cosas que hay en total: ¿Cuántos huevos tiene en total?
Para resolver este problema, debemos pensar:
-Si en cada caja hay 12
huevos y Ana tiene 5 cajas, para saber cuántos huevos hay en total, sumaremos
12 + 12 + 12 + 12 + 12 o, lo que es lo mismo, multiplicaremos 5 x 12:
-En
total, Ana tiene 60 huevos
2. Problemas de multiplicación:
Escalar de comparación
En este tipo de problemas de multiplicación se compara una cantidad con otra que
es más grande o más pequeña:
Para
comprar el regalo de su padre, Juan ha puesto 10.000 pesos y Patricia ha puesto 3
veces más dinero que él.
¿Cuánto dinero ha puesto
Patricia?
Encontraremos:
– Un número que expresa una cantidad: Juan ha puesto 10.000 pesos.
– Un número que expresa la comparación entre la segunda
cantidad y la primera: Patricia ha puesto 3 veces más dinero que Juan
– La pregunta sobre la segunda cantidad: ¿Cuánto dinero ha puesto Patricia?
Para resolver el problema, debemos pensar:
Si Patricia ha puesto 3
veces más dinero que Juan, quiere decir que habrá puesto el triple de dinero.
Por eso, multiplicaremos 10.000 x 3:
Patricia ha puesto 30.000 pesos.
3. Problemas de multiplicación:
Escalar de fórmula
En este tipo de problemas de multiplicación nos aparecerán fórmulas, como por
ejemplo una velocidad:
Sergio
es conductor de autobús. Me ha dicho que, si no hiciese ninguna parada y
mantuviese siempre la velocidad de 80 kilómetros por hora, tardaría en hacer su
recorrido exactamente 2 horas. ¿Cuántos kilómetros mide su recorrido?
Encontraremos:
– Una velocidad: Si mantuviese la velocidad
de 80 kilómetros por hora
– Un tiempo: Tardaría 2 horas
– Una pregunta sobre la distancia: ¿Cuántos kilómetros mide
su recorrido?
Para resolver el problema, debemos pensar: si mantiene
una velocidad de 80 kilómetros por hora, quiere decir que cada hora que conduce
recorre 80 kilómetros. También sabemos que conduce a esta velocidad durante 2
horas. Por lo tanto, para saber el número de kilómetros que recorre en total,
tendremos que multiplicar 80 x 2:
Su recorrido mide 160 kilómetros.
-En este tipo de problemas de multiplicación encontraremos dos o más conjuntos de cosas o personas.
-Estos conjuntos se deben combinar entre sí formado todas las parejas posibles:
Hoy
hemos ido a comer a un restaurante italiano especializado en pasta. Me ha
costado mucho decidir qué plato pedir, ya que en la carta había 9 tipos de
pasta y 11 tipos de salsa, y se podía pedir cualquier pasta con cualquier
salsa.
¿Entre cuántos platos distintos de pasta con salsa se podía elegir?
Encontraremos:
– El número de elementos que tiene el primer conjunto: 9 tipos de pasta
– El número de elementos que tiene el segundo conjunto: 11 tipos de salsa
– La pregunta, que se refiere al número de combinaciones
posibles entre los conjuntos: ¿Entre cuántos platos distintos de pasta con salsa se podía elegir?
Para resolver el problema, debemos pensar:
-Cada tipo de pasta podríamos combinarla con los 11 tipos de salsa disponibles. Por lo tanto, solo con el primer tipo de pasta podemos obtener 11 platos distintos.
-Cada tipo de pasta podríamos combinarla con los 11 tipos de salsa disponibles. Por lo tanto, solo con el primer tipo de pasta podemos obtener 11 platos distintos.
-Combinando el segundo tipo de pasta con cada una de las 11 salsas, también
obtendríamos otros 11 platos distintos. Es decir, por cada uno de los 9 tipos
de pasta, obtendremos 11 platos distintos al combinarlos con las salsas.
-Por
ello, para averiguar el número de platos posibles, multiplicaremos 9 x 11: Se podía elegir entre 99 platos distintos de
pasta
Problemas:
1.- En cada aula de un
colegio hay entre 25 y 30 sillas. Si en ese colegio hay 14 aulas. ¿Cuántas
sillas habrá como mínimo? ¿Y como máximo?
2.- Cuatro decenas de huevos
y seis huevos más. ¿Cuántos huevos son?
3.- Cuatro kilos de patatas
y 5 sacos de 6 kilos cada uno, ¿cuántos kilos de patatas son?
4.- Laura es piloto
comercial. Cada semana realiza cinco viajes de ida y vuelta entre Alicante y
Vitoria. La distancia entre ambas ciudades es de 730 Km. Laura estima que en
seis semanas recorre más de 40.000 Km, que es como dar la vuelta al mundo.
¿Tiene razón Laura?
5.- Un grifo estropeado pierde un litro de
agua cada media hora. ¿Cuánto perderá cada hora? ¿Cuánto perderá al cabo de un
día? Si no se repara. ¿Cuántos litros se perderán en un mes?
6.- Una camisa tiene siete
botones en la parte delantera, dos en el cuello, uno en cada puño y un botón de
repuesto. Si una fábrica hace cada día 20 camisas de manga larga y otras 20 de
manga corta. ¿Cuántos botones gastan en un día? ¿Tendrán suficiente con 2.000
botones para los cinco días de una semana?
7.- Una charca contiene
3.000 litros de agua, y en ella beben vacas y ovejas. Cada día, una oveja bebe
2 litros de agua y una vaca bebe 8 litros. Si al cabo de un día pasan por la
charca 253 ovejas y 117 vacas, ¿habrá agua para todas?
Dividir es
repartir un número en grupos iguales (del tamaño que indique el divisor).
Por ejemplo:
45 : 5 es repartir 45 en grupos de 5.
Los términos
de la división son:
· -Dividendo: es el número que vamos a dividir.
· -Divisor: es el número por el que vamos a dividir.
· -Cociente: es el resultado.
· - Resto: la parte que no se ha podido distribuir.
División por una cifra:
Por ejemplo:
-Queremos repartir 243 caramelos entre 5
amigos.
-El dividendo será 243 porque es la cantidad que queremos dividir.
-El
divisor es 5 porque es el número por el que queremos dividir (repartir) los 243
caramelos.
-El cociente será el número de caramelos que recibe cada niño y el
resto son los caramelos que sobran.
Vamos a ver los pasos para calcular el cociente y el
resto:
1. Cogemos la primera cifra del
dividendo. Si esta cifra es más pequeña que el divisor, entonces tendremos que
coger otra cifra más del dividendo.
En nuestro ejemplo la primera cifra del dividendo es
2, pero como es más pequeña que el divisor, que es 5, tenemos que coger otra
cifra más: 24
2. Buscar un número que al
multiplicarlo por el divisor nos dé como resultado el dividendo. Si no lo hay,
buscamos el resultado menor más próximo. El resultado de la multiplicación se
resta al dividendo.
-Nosotros tenemos que dividir 24 entre 5.
Buscamos un
número que multiplicado por 5 me dé 24. Como no es exacto buscamos el menor más
próximo: 4 x 5 = 20.
-En este caso, 20 es el número más cercano a 24 siendo
menor. Por lo tanto escribimos el 4 en el cociente y el 20 se lo restamos a 24,
y 20 – 24 = 4
3. Bajar la siguiente cifra del dividendo y realizar de nuevo el paso
2.
-Bajamos la siguiente cifra que es el 3. Con el 4 que
ya teníamos y con el 3 que acabamos de bajar obtenemos el 43.
-Ahora dividimos 43 entre 5.
-Buscamos un número que
multiplicado por 5 nos dé 43.
Como no es exacto buscamos un número que no dé el
número menor más próximo.
-En este caso 5 x 8 = 40. Escribimos el 5 en el
cociente y el 40 lo escribimos debajo del 43 para restarlo: 43 – 40 = 3.
Como no hay más cifras en el dividendo, hemos
terminado la división.
Por lo tanto, cada niño recibe 48 caramelos y sobran 3
caramelos sin repartir.
División por dos o tres cifras:
Para
hacer divisiones de dos o tres cifras hay que seguir los siguientes pasos:
1- Coger tantas cifras del dividendo como cifras tenga el
divisor. Si las cifras del dividendo son más pequeñas que el divisor, hay que
coger otra cifra más en el dividendo.
Por
ejemplo:
Si queremos dividir 5738 / 73, lo primero que tenemos que hacer es
coger dos cifras del dividendo, 57, pero como 57 es menor que 73, hay que coger
otra cifra más del dividendo, es decir, 573.
2- Dividir el primer número del dividendo (o los dos
primeros si hemos tenido que coger otra cifra) entre el primer número del
divisor y comprobar si cabe. Si no cabe, comprobar con el número anterior.
-Si
seguimos con el ejemplo anterior, tendríamos que dividir 57 entre 7. Como 8 x 7
= 56, probaremos con 8.
-Multiplicamos 73 x 8 = 584 y como 584 es mayor que 573,
el 8 no cabe, por lo que tendríamos que probar con el número anterior.
73 x
7 = 511 y como 511 es más pequeño que 573, el 7 si cabe y podríamos hacer la
resta de 573 – 511 = 62.
3- Bajar la cifra siguiente y dividir como en el paso
anterior hasta que no haya más cifras.
-Seguimos
con nuestro ejemplo de división por dos cifras. El siguiente número que
tendríamos que bajar es el 8, por lo que ahora tendríamos que dividir 628 entre
73.
-Cogemos otra vez las dos primeras cifras 62 y tendríamos
que dividirlas entre 7. Como 8 x 7 = 56, escribimos 8 en el cociente y
multiplicamos 73 x 8 = 584.
-Como 584 es más pequeño que 628, procedemos a hacer
la resta 628 – 584 = 44. Como ya no hay más números que bajar, hemos terminado
la división.
-El resultado es 78 y el resto es 44.
Cómo resolver problemas de divisiones:
Vamos a plantear varios problemas diferentes que
requieran de una división para su resolución.
Problema 1.
En el colegio algunos profesores se habían quejado de
que no había suficiente material, y por eso se han repartido
18 cajas de gomas de borrar a partes iguales entre 9 clases.
¿Cuántas cajas de gomas de borrar recibirá cada clase?
*Este es el tipo de problema más fácil que nos podemos
encontrar sobre divisiones. El problema nos dice que hay 18 cajas y se quieren repartir a partes iguales entre 9 clases.
Cuando hablemos de repartir
a partes iguales estamos hablando de DIVIDIR.
18: 9 = 2
R//. Cada clase recibirá 2 cajas de gomas de borrar.
Problema
2.
En el
depósito de agua que hay al lado de los grandes jardines de mi pueblo en lo más
alto de una colina, que está ahí para que haya suficiente agua para los riegos,
solo quedan 56 litros de agua. Si se reparte
toda en recipientes de 8 litros cada uno,
¿cuántos
recipientes se llenarán?
Este problema es parecido al anterior. De nuevo hay que repartir los 56 litros de agua en recipientes de 8 litros cada uno. Por lo tanto, lo que tenemos que hacer es DIVIDIR.
Este problema es parecido al anterior. De nuevo hay que repartir los 56 litros de agua en recipientes de 8 litros cada uno. Por lo tanto, lo que tenemos que hacer es DIVIDIR.
56: 8 = 7
R//. Se llenarán 7 recipientes.
Problema
3.
Como
todos los domingos por la mañana, Ricardo y Catalina han salido a andar por el
campo. Como están acostumbrados a hacer deporte, van rápido y sin hacer paradas
en el camino.
Sabiendo
que la caminata dura 3 horas, que en total caminan 15 kilómetros y que se han
cruzado con 7 personas, calcula a qué velocidad caminan.
Hay que empezar aclarando en este problema que la
velocidad se mide en km/h (se lee kilómetros por hora), y se refiere a los
kilómetros que se recorren en una hora.
El problema nos dice que recorren 15 kilómetros y que
han tardado 3 horas. El dato de las 7 personas con las
que se cruzaron no es importante para este problema.
Por lo tanto, si en 3 horas hace 15 kilómetros,
¿cuántos kilómetros habrá hecho en una hora?
Para hallarlo tendremos que DIVIDIR.
15: 3 = 5
R//. Ha ido a una velocidad de 5 km/h.
Problema
4.
Raimundo
y yo estamos ahorrando para comprar un juego entre los dos y regalárselo a
Carmen por su cumpleaños, que va a ser dentro de 5 días. Él ha conseguido 90.000 pesos y yo ya tengo 270.000
¿Cuántas
veces he ahorrado yo más dinero que Raimundo?
El lenguaje del problema puede llevar a
interpretaciones erróneas, ya que veces más o veces menos puede interpretarse
como una suma o resta pero siempre van asociados a problemas de
multiplicaciones o divisiones.
En el caso concreto de este problema, nos dicen que
Raimundo ha conseguido 90.000 pesos y que yo tengo 270.000 pesos y me preguntan por las
veces que he ahorrado yo más que él.
Raimundo ha conseguido menos dinero que yo, por lo
tanto la cantidad que él tiene (90.000 pesos) multiplicada por otra cantidad (veces
más) tiene que dar como resultado el dinero que tengo yo (270.000 pesos). Por lo
tanto, lo que tenemos que hacer es DIVIDIR.
270.000: 90.000 = 3
Yo he ahorrado 3 veces más dinero que Raimundo.
Potencia
de un número es multiplicar dicho número por sí mismo tantas veces como indique
el exponente.
*La potencia se lee "base elevado al exponente".
Los 3 ejemplos anteriores se leen:
2 elevado a 5
3 elevado a 4
5 elevado a 6
*Potencia en base 10
Un caso particular de potencia es cuando la base es 10.
Como se puede
apreciar en los ejemplos anteriores, en la potencia en base 10 el resultado
siempre es igual a 1 seguido de tantos ceros como indique el exponente.
En el primer
ejemplo un 1 seguido de 5 ceros
En el segundo
ejemplo un 1 seguido de 4 ceros
En el tercer
ejemplo un 1 seguido de 6 ceros.
La radicación es en realidad otra forma de
expresar una potenciación.
La raíz de cierto orden de un número es
equivalente a elevar dicho número a la potencia inversa.
Por esto, las propiedades de
la potenciación se cumplen también con la radicación. Para que estas
propiedades se cumplan, se exige que el radicando de las raíces sea positivo.
• Es distributiva con respecto a la multiplicación y a la
división.
Veamos un ejemplo:
-En la división
-En la multiplicación
• No es distributiva con respecto
a la suma y a la resta.
Ejemplos:
En la suma
En la resta
• Si el índice es par entonces el
radicado tiene que ser positivo y la raíz entonces dos
resultados, uno positivo y otro negativo, para este nivel utilizamos el
resultado positivo.
Ejemplos
Si el índice es impar entonces la raíz va
a tener el mismo signo que el radicando:
Si tengo una raíz de raíz se multiplican
los índices:
Ejercicio:
El logaritmo
de un número real cualquiera es el exponente al que hay
que elevar la base para obtener dicho resultado.
Ejemplo
Propiedades de la logaritmación
1) El logaritmo de un cociente es igual a la
diferencia entre los logaritmos de dividendo y divisor.
2) El logaritmo de un producto es igual a la suma entre los
logaritmos de los factores.
3) El
logaritmo de una potencia es igual al producto del exponente por el logaritmo
de la base.
4) El logaritmo de una raíz es igual al
logaritmo del radicando dividido el índice de la raíz.
5) El logaritmo de 1 es 0
6) No existe el logaritmo de 0.
7) No existe el logaritmo de un número negativo.
Ejercicios
Vamos a estudiar varios
tipos de figuras planas:
1.- Polígono: todos sus lados son líneas rectas.
Un polígono es una línea
poligonal cerrada.
Veamos algunos ejemplos:
En cambio, las siguientes figuras no son
polígonos:
a) Porque son figuras abiertas:
b) Porque tiene líneas curvas:
*Los polígonos se clasifican por el número de lados:
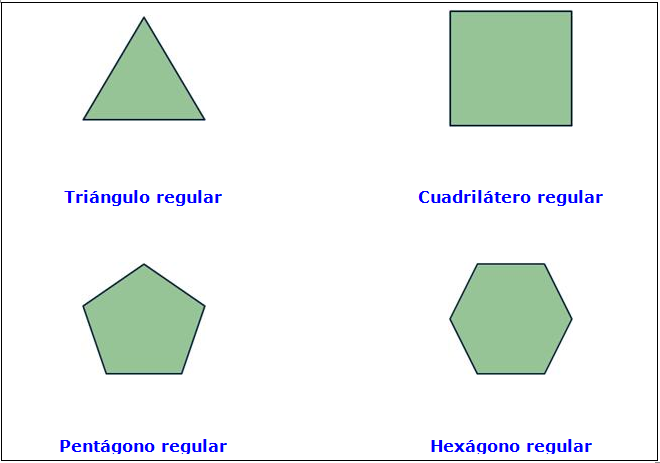
*Si todos los lados de un polígono son iguales se llama: polígono regular:
-Triángulo regular: 3 lados iguales
-Cuadrilátero regular: 4 lados iguales
-Pentágono regular: 5 lados iguales
-Hexágono regular: 6 lados iguales
-Cuadrilátero regular: 4 lados iguales
-Pentágono regular: 5 lados iguales
-Hexágono regular: 6 lados iguales
Los polígonos regulares son simétricos,
tienen eje de simetría, es decir un eje que divide la figura en dos parte
iguales:
2.- Los cuadriláteros: El cuadrilátero es un polígono de cuatro lados y cuatro vértices.
Según las relaciones que se establecen entre sus lados y entre sus ángulos, pueden distinguirse tres tipos de cuadriláteros
-paralelogramos
-trapecios y
-trapezoides
3.- El cuadrado: El cuadrado es un tipo de rectángulo. Tienen las mismas características pero además los 4 lados del cuadrado miden igual.
Forma parte del conjunto de los cuadriláteros (tiene
cuatro lados) y de los paralelogramos (ya que
estos cuatro lados son paralelos).
Otra
particularidad de un cuadrado es que sus cuatro ángulos interiores son rectos (es decir, miden 90º).
4.- El rectángulo: es un polígono formado por 4 rectas llamadas lados. Las características de los rectángulos son que sus lados opuestos son paralelos y sus 4 ángulos miden 90º.
Los ángulos de un rectángulo son todos
iguales y rectos. Suman en total 360 grados.
*La fracción se
utiliza para representar las partes que se toman de un objeto que ha sido
dividido en partes iguales.
Los términos de la fracción se denominan: numerador y denominador.
¿Cómo se leen las fracciones? Se leen en función de cuál es su denominador:
1 / 2: un medio
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
1 / 3: un tercio
1 / 4: un cuarto
1 / 5: un quinto
1 / 6: un sexto
1 / 7: un séptimo
1 / 8: un octavo
1 / 9: un noveno
1 / 10: un décimo
1 / 11: un onceavo
1 / 12: un doceavo
1 / 13: un treceavo
Actividad:
*Fracción mixta:
Para convertir una
fracción impropia en número mixto, se divide el numerador entre el denominador,
y el cociente es el número natural. El resto de la división es el numerador de
la fracción propia que falta para completar el número mixto. El denominador se
mantiene el de partida.
*Fracción equivalente:
Dos fracciones son
equivalentes cuando equivalen a las mismas unidades.
Por ejemplo:
Estas dos fracciones son equivalentes ya que equivalen a las mismas unidades:
4 : 8 = 0,5 unidades
1 : 2 = 0,5 unidades
¿Cómo sabemos cuándo dos fracciones son
equivalentes?
Para ello dividimos sus
numeradores y sus denominadores, si guardan la misma proporción es que son
equivalente:
Veamos un ejemplo:
Dividimos sus numeradores: 6
: 2 = 3
Dividimos sus denominadores:
9 : 3 = 3
Guardan la misma proporción (3) luego
estas dos fracciones son equivalentes.
Podemos comprobarlo.
La primera fracción equivale
a 6 : 9 = 0,66 unidades
La segunda fracción equivale
a 2 : 3 = 0,66 unidades
Más ejemplos:
Más ejemplos:
-Dividimos sus numeradores: 2 : 3 = 0,66
-Dividimos
sus denominadores: 4 : 9 = 0,44
-No
guardan la misma proporción luego estas dos fracciones no son equivalentes.
-Podemos
comprobarlo.
-La
primera fracción equivale a 2 : 4 = 0,50 unidades
La
segunda fracción equivale a 3 : 9 = 0,33 unidades
*Amplificación de fracciones
Amplificar una fracción consiste en encontrar una fracción equivalente pero
con sus términos (numerador y denominador) mayores.
Para amplificar una fracción basta con multiplicar el numerador
y el denominador por el mismo número
Ejemplo :
Luego
las fracciones 3 y 18 son
equivalentes.
5 30
*Simplificación de fracciones
Luego las fracciones 3 y 18 son equivalentes.
5 30
*Simplificación de fracciones
Simplificar una fracción consiste
en encontrar una fracción equivalente pero con sus términos(numerador y
denominador) más pequeños.
Para simplificar una fracción debe existir un número
entre el que podamos dividir el numerador y el denominador de manera exacta.
Es decir, para poder simplificar una fracción el numerador y el denominador
tienen que tener algún divisor común (no pueden ser primos entre sí).
Ejemplos de los dos casos:
Simplificar una fracción consiste
en encontrar una fracción equivalente pero con sus términos(numerador y
denominador) más pequeños.
Ejemplos de los dos casos:
Las fracciones que no se pueden simplificar más
se les llama irreducibles,
esto sucede cuando el numerador
y el denominador son primos entre sí.
-Aunque se puede empezar a simplificar dividiendo por cualquier número, se debe
seguir un orden lógico (por ejemplo los primos: 2, 3, 5, ..), es decir,
probamos dividir ambos entre 2 mientras se pueda, después pasamos al 3 y así
sucesivamente.
*Datos importantes:
- El
numerador y el denominador de la fracción siempre deben ser
números enteros.
- Las
operaciones que podemos hacer son multiplicar y dividir (siempre las dos partes
a la vez). Si sumamos o restamos un número arriba y abajo, no tendremos una fracción equivalente.
- El
número que elijas para dividir las dos partes no debe dejar ningún resto en las
divisiones.
Las fracciones que no se pueden simplificar más se les llama irreducibles, esto sucede cuando el numerador y el denominador son primos entre sí.
1- ¿Cómo se comparan las fracciones?
1.1- Fracciones con igual denominador
De dos fracciones que tienen el mismo
denominador es menor la que tiene menor
numerador.
Ejemplo:
1.2- Fracciones con igual numerador
De dos fracciones que
tienen el mismo numerador es menor el que
tiene mayor denominador.
Ejemplo:
1.3- Con numeradores y denominadores distintos
-En primer
lugar las tenemos que poner a común denominador.
Es menor la que tiene menor numerador.
Para sumar y restar fracciones hay que distinguir entre:
-Fracciones con igual
denominador
-Fracciones con distinto
denominador
1.- Fracciones
con igual denominador
En este caso para sumar o
restar fracciones se mantiene constante el denominador y se suman o restan sus
numeradores.
a)
Veamos un ejemplo:
Sumamos sus numeradores y mantenemos el denominador:
a)
Veamos otro ejemplo:
Restamos sus numeradores y mantenemos el
denominador:
Restamos sus numeradores y mantenemos el denominador:
2.- Fracciones con
distinto denominador
En este caso para sumar o restar fracciones:
Y ¿cómo se calcula este denominador común?
Una manera sencilla de calcularlo es multiplicar todos los
denominadores; el resultado es el denominador común.
Ejemplos:
2.- Fracciones con distinto denominador
En este caso para sumar o restar fracciones:
Lo primero que hay que hacer es buscar un denominador común a
todas ellas.
Luego sustituir las fracciones originales por fracciones
equivalentes con este denominador común.
Y ¿cómo se calcula este denominador común?
Una manera sencilla de calcularlo es multiplicar todos los
denominadores; el resultado es el denominador común.
Hay una forma más correcta de calcularlo a través del mínimo
común múltiplo. Es una forma más compleja que queda para cursos superiores.
Una vez obtenido el denominador común hay que calcular las
fracciones equivalentes. Para cada fracción haremos lo siguiente.
Sustituimos su denominador por el denominador común.
Ejemplos:
Ejemplos:
1.- Multiplicación de fracciones
Para multiplicar fracciones:
Se multiplican sus numeradores y sus denominadores:
Vamos a ver otros ejemplos:
Ejercicios:
2.- División de fracciones
Cuando se dividen 2 fracciones:
La fracción resultante
tendrá:
-Como numerador: el resultado de multiplicar el
numerador de la primera por el denominador de la segunda.
-Como denominador: el resultado de multiplicar el
denominador de la primera por el numerador de la segunda.
Vamos a ver otros ejemplos:
Figuras bidimensionales:
Figuras tridimensionales:
En los números enteros la cifra más pequeña es la unidad:
Pero también hay números que tienen una parte inferior a
la unidad, estos se llaman números decimales:
La parte entera va a la izquierda de la coma y la parte
decimal a la derecha.
Vamos a ver cada una de estas cifras decimales
a) La décima
a) La décima es un valor más
pequeño que la unidad.
1 unidad = 10 décimas.
Es decir, si dividimos una unidad en 10 partes iguales, cada una de ellas
es una décima.
Las décimas van a la derecha de la coma.
b) La centésima es un valor más pequeño que la unidad y también que la décima.
1 unidad = 100 centésimas
Es decir, si dividimos una unidad en 100 partes iguales, cada una de ellas
es una centésima.
Y si dividimos una décima en 10 partes iguales, cada una de ellas es una
centésima.
c) La milésima es un valor más pequeño que la unidad, que la décima y también que la
centésima:
1 unidad = 1.000 milésimas
Es decir, si dividimos una unidad en 1.000 partes iguales, cada una de
ellas es una centésima.
Existen dos modos diferentes:
*Se lee primero la parte entera indicando
las unidades que son y a continuación la cantidad decimal indicando el orden de
la última cifra decimal.
* Leer la parte entera y la parte decimal
separadas por la palabra coma.
Es decir, si dividimos una unidad en 1.000 partes iguales, cada una de
ellas es una centésima.
Existen dos modos diferentes:
*Se lee primero la parte entera indicando
las unidades que son y a continuación la cantidad decimal indicando el orden de
la última cifra decimal.
* Leer la parte entera y la parte decimal
separadas por la palabra coma.
Más ejemplos:
53,41 se puede leer de varias maneras:
-Cincuenta y tres coma cuarenta y uno.
-Cincuenta y tres con cuarenta y uno.
-Cincuenta y tres unidades y cuarenta y una centésimas.
Se escribe primero la parte entera seguida de una coma y después la parte decimal
42 unidades y 12 milésimas = 42,012
Todos los ceros situados en la parte izquierda de la parte decimal se pueden eliminar.
Para comparar números decimales puedes
comparar las partes enteras de los números decimales entre sí y
luego las cifras decimales según su posición, comenzando por la de mayor
valor (décimos), hasta que una de ellas sea de menor o mayor
que la otra.
Por ejemplo
comparar 4,25 y 4,21
Otro caso es cuando tenemos números
decimales, con distintas cantidades de cifras decimales después de la
coma.
Para comparar si un número decimal es mayor, menor o
igual a otro podemos igualar con ceros las cifra decimales para que cada
cantidad tenga el mismo número de cifras decimales después de la coma.
Ya igualadas las cifras procedemos a comparar y a
ubicar en la posición que le corresponde.
En el siguiente ejemplo queremos saber Cuál número es mayor entre 0,2 y 0,85.
Observa en la gráfica que lo primero que se hace es igualar el número de cifras
decimales agregando ceros a la derecha, para luego poder compararlas.
Ampliando la explicación:
Para
comparar números decimales comenzamos comparando la parte entera: aquél que
tenga la parte entera más alta, es el mayor.
234,65 es
mayor que 136,76
Si ambos
tienen igual parte entera habría que comparar la parte decimal, comenzando por
las décimas, luego las centésimas y por último las milésimas.
Veamos
algunos ejemplos:
146,89 es
mayor que 146,78 (ambos tienen igual parte entera, pero el primero tiene 8
décimas mientras que el segundo tiene 7).
357,56 es
mayor que 357,53 (ambos tienen igual parte entera y también las mismas décimas,
pero el primero tiene 6 centésimas y el segundo tan sólo 3).
634,128 es
mayor que 634,125 (ambos tienen igual parte entera y también las mismas
décimas y centésimas, pero el primero tiene 8 milésimas y el segundo tan sólo
5).
Veamos otros ejemplos:
* Vamos a
comparar un número con parte decimal y otro sin parte decimal:
207,12 es
mayor que 207 (ambos tienen igual parte entera, pero el primero tiene 1 décima
mientras que el segundo no tiene ninguna).
* Vamos a
comparar un número con décimas y centésimas y otro sólo con décimas:
43,28 es
mayor que 43,2 (ambos tienen igual parte entera y las mismas décimas, pero el
primero tiene 8 centésimas mientras que el segundo no tiene ninguna).
* Vamos a
comparar un número con décimas y otro sólo con centésimas:
72,1 es
mayor que 72,09 (ambos tienen igual parte entera, pero el primero tiene 1 décima
y el segundo ninguna).
1. Suma
La suma y resta con números decimales es
exactamente igual que con números enteros. Lo único que hay que vigilar es que
cada tipo de cifra vaya en su columna:
Las centenas en la columna de centenas,
las decenas en la de decenas, las unidades en la de unidades, las décimas en la
de décimas, las centésimas en la de centésimas.
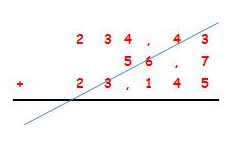
Vamos a ver un ejemplo:
234,43 + 56,7 + 23,145
Podemos ver que todas las cifras van en
su columna correspondiente.
También las comas van todas en la misma
columna.
Un fallo que se suele cometer al operar
con números decimales es alinear todos los números a la derecha:
Esta suma está mal escrita, ya que el 3
de la primera fila (centésima) lo estamos sumando con el 7 de la segunda fila
(décima) y con el 5 de la tercera fila (milésima).
La operatoria, como hemos comentado, es
exactamente igual que con números enteros:
Puede ocurrir, como en el ejemplo, que
en la suma o en la resta haya algún número que no lleve todas las cifras
decimales (por ejemplo, el tercer número del ejemplo no lleva centésimas), en
este caso operamos como si en su lugar hubiera un 0.
2. Resta
2. Resta
La resta, al igual que la
suma, funciona exactamente igual que con números enteros.
Como hemos indicado
anteriormente, si algún número no lleva todas su cifras decimales (en este
ejemplo, el primer número 157,83 no lleva milésimas) se opera como si en su
lugar hubiera un 0.
Actividad
Actividad
3. Multiplicación
En una multiplicación puede haber decimales en
cualquiera de los dos factores, o en los dos:
a) En primer lugar
multiplicamos sin tener en cuenta que hay decimales:
b) A continuación contamos los números decimales que hay en ambos factores
y serán las cifras decimales que lleve el resultado:
b.1.- Empecemos por la primera multiplicación:
Tiene una
cifra decimal en el primer factor y ninguna en el segundo: en total 1 cifra
decimal.
El resultado
de la multiplicación (324.324) llevará 1 cifra decimal:
b.2.- Segunda multiplicación
Tiene dos cifras decimales en el segundo factor: en
total 2 cifras decimales.
El resultado de la multiplicación (527.814) llevará 2
cifras decimales:
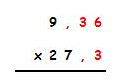
b.3.- Tercera
multiplicación
Tiene dos cifras decimales
en el primer factor y una en el segundo: en total 3 cifras decimales.
El resultado de la multiplicación (255.528) llevará por tanto 3 cifras
decimales:
Multiplicar por 10, 100, 1.000
Por ejemplo:
45,6 x 10
235,6 x 100
78,96 x 1.000
Para calcular el resultado:
a) Primero escribimos en el resultado el primer
factor.
b) Luego en el resultado desplazaremos la coma a la
derecha tantas posiciones como ceros lleve el número por el que hemos
multiplicado.
Puede ocurrir que haya más ceros que cifras decimales,
por lo que no podamos desplazar a la derecha la coma tantas posiciones como
ceros.
¿Qué hacemos?
Las posiciones que no hayamos podido
desplazar la coma la completaremos con ceros:
Veamos los ejemplos:
a) 45,6 x 10
Primeros repetimos en el resultado el primer factor.
45,6 x 10 = 45,6
Luego desplazaremos la coma a la derecha una posición
ya que hemos multiplicado por 10 que lleva 1 cero:
45,6 x 10 = 456, (la coma a la derecha sin ninguna
cifra decimal se puede quitar y escribir 456)
b) 235,6 x 100
Primeros repetimos en el resultado el primer factor.
235,6 x 100 = 235,6
Luego desplazaremos la coma a la derecha dos
posiciones ya que hemos multiplicado por 100 que lleva 2 ceros:
Como 235,6 tan sólo tiene un decimal y necesitamos
desplazar la coma 2 posiciones, completaremos el movimiento que nos falta
poniendo 1 cero:
235,6 x 100 = 23.560
c) 78,96 x 1.000
Primeros repetimos en el resultado el primer factor.
78,96 x 1.000 = 78,96
Luego desplazaremos la coma a la derecha tres
posiciones ya que hemos multiplicado por 1.000 que lleva 3 ceros.
Como 78,96 tan sólo tiene dos decimales y necesitamos
desplazar la coma 3 posiciones, completaremos el movimiento que nos falta
poniendo 1 cero:
78,96 x 1.000 = 78.960
Ejercicios
1. Realiza las siguientes operaciones:
4. División
1- Número decimal entre número entero: Se dividen como si fuesen enteros.
En la división al bajar el primer
número decimal, se escribe la coma en el cociente. Vamos a ver un ejemplo,
dividiendo 77,5 entre 25.
- 77 entre 25 es igual a 3.
- 3 x 5 = 15, al 7 van 2 y me llevo 1.
- 3 x 2 = 6 y una que me llevaba, son 7. Por lo
tanto, al 7 son 0.
- Ahora bajamos la siguiente cifra.
Como el 5 es el
primer número decimal, escribiremos la coma en el cociente. Y dividimos, 25
entre 25, que es igual a 1.
1 x 25 = 25, al 25 van 0.
Y el resultado de esta división de número decimal
entre entero es: 3,1
2- Número entero entre número decimal: Se quita la coma del divisor y se añaden al dividendo tantos ceros como decimales había.
Por ejemplo, vamos a dividir 278 entre 3,6.
En el divisor no puede haber decimales, por lo
tanto, quitamos la coma y añadimos al dividendo tantos ceros como decimales
tiene el divisor.
- En este caso tenemos que añadir un solo cero.
- Y ahora tenemos
que dividir 2780 entre 36.
- 278 entre 36, que es igual a 7.
- 7 x 6 = 42, al 48 van 6 y me llevo 4.
- 7 x 3 = 21 y 4 que me llevaba son 25, al 27 son 2.
- Ahora bajamos el 0, por lo que dividimos 260 entre
36, que es igual a 7.
- 7 x 6 = 42, al 50 van 8 y nos llevamos 5.
- 7 x 3 = 21 más 5 que nos llevábamos son
26, al 26 van 0.
El resultado de la división es 77 y de resto 8.
3- Número decimal entre número decimal: Se quita la coma del divisor y se mueve la coma del dividendo hacia la derecha, tantas posiciones como decimales tenga el divisor. Ahora vamos a dividir 278,1 entre 2,52.
Primero quitamos la coma del divisor y como el divisor tiene dos decimales, hay que mover la coma del dividendo dos posiciones.
Como el dividendo solo tiene un decimal, hay que añadir tantos
ceros como posiciones nos falten.
En este caso, añadimos un cero. Y ahora
dividimos 27810 entre 252.
- 278 entre 252 es igual a 1.
- 1 x 2 = 2, al 8 van 6.
- 1 x 5 = 5, al 7 van 2.
- 1 x 2 = 2, al 2 van 0.
Bajamos el siguiente número que es un 1, por lo que
ahora tenemos que dividir 261 entre 252, que es 1.
- 1 x 2 = 2, al 11 van 9 y me llevo 1.
- 1 x 5 = 5, y 1 que me llevaba son 6, al 6 van 0.
- 1 x 2 = 2, al 2 van 0.
- Bajamos el siguiente número que es un 0, por lo que
ahora tenemos que dividir 90 entre 252.
- Como 90 es más pequeño que 252, tenemos
que escribir 0 en el cociente y bajar la cifra siguiente. Como no hay más
cifras, ya hemos terminado de realizar la división. Y el resultado sería 110 y
de resto 90.
- Ahora
vamos a ver cómo sacar decimales.
Si al
terminar la división nos ha quedado resto, escribimos una coma en el cociente y
añadimos un cero en el dividendo. Si queremos seguir sacando decimales, habrá
que ir añadiendo ceros en el dividendo. Vamos a ver un ejemplo de sacar
decimales, dividiendo 33 entre 6.
- 33 entre 6 es igual a 5.
- 5 x 6 = 30, al 33 van 3.
Nos quedaríamos con un resto de 3.
- Por lo que si
queremos añadir decimales, tenemos que poner una coma en el cociente, detrás
del 5 y añadimos un cero al resto.
- Ahora tendríamos que dividir 30 entre 6, que
es igual a 5.
5 x 6 = 30, al 30 van 0.
Y el resultado de 33 entre 6 es igual a 5,5.
Si quieres ver el video tutorial completo de divisiones con números decimales, haz clic en el enlace.
Si quieres ver el video tutorial completo de divisiones con números decimales, haz clic en el enlace.
Ejercicios:
ESTADÍSTICA
Es la ciencia de recoger, clasificar, describir y analizar datos que sirven para deducir conclusiones y tomar decisiones de acuerdo con esos análisis.
Es el número de veces que se repite un dato. Cuando se recogen información obtenemos un gran número de datos que se puede presentar en una tabla de frecuencias.
Tamaño de la muestra:
Es el número total de los datos recogidos.
Frecuencia Absoluta:
En el grado 5b se recogió la siguiente información: No tengo hermanos, tengo 2 hermanos, tengo 1 hermano, tengo 3 hermanos, tengo 2 hermanos, tengo 2 hermanos, tengo 4
hermanos, tengo 6 hermanos, tengo 2 hermanos, tengo 1 hermano, tengo 1 hermano, tengo 2 hermanos, tengo 2 hermanos, tengo 2 hermanos, tengo 2 hermanos, tengo 1 hermano, tengo 1 hermano, tengo 1 hermano, tengo 5 hermanos, tengo 1 hermano, tengo 1 hermano, tengo 3 hermanos, tengo 1 hermano, tengo 1 hermano, tengo 2 hermanos, tengo 2 hermanos, tengo 2 hermanos, tengo 3 hermanos.
Tabla de Frecuencia
Frecuencia Relativa:
La frecuencia relativa es el resultado de dividir la frecuencia absoluta entre el tamaño de la muestra.
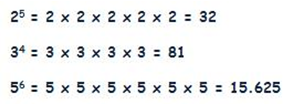
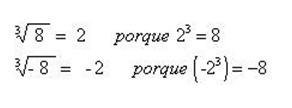
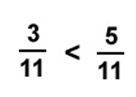
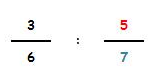
No hay comentarios:
Publicar un comentario